
Basics of Satellite Communication - the Linked Budget
17 October 2022
Quetsilquatl
Opening Remarks
On this page, we look at an overall wireless communication system. A big part of designing and maintaining a communication system involve a Linked Budged Analysis. We will discuss how to break down the Linked Budget and how to understand the different figures.
Gain and Loss
The ultimate goal of the Linked Budget Analysis is to find the power received. This analysis consists of two main pieces: Gain and Loss. When we've completed the analysis, we then can use it as a tool for design criteria, but we can use it for troubleshooting the system. Equation 1 demonstrates the Linked Budget Equation. The budget is usually evaluated with decibels to simplify the calculation.
Equation 1 $$P_{r} = P_{t} + G_{t} + G_{r} - L_{p} - L_{r}$$
$P_{r} = $ Power received at Receiver
$P_{t} = $ Power transmitted at Transmitter
$G_{r} = $ Gain of Receiver
$G_{t} = $ Gain of transmitter
$L_{p} = $ Path Loss
$L_{r} = $ Additional Losses
Equation 1 can be simplified further to include EIRP as shown in Equation 2
Equation 2 $$P_{r} = EIRP + G_{r} - L_{p} - L_{r}$$
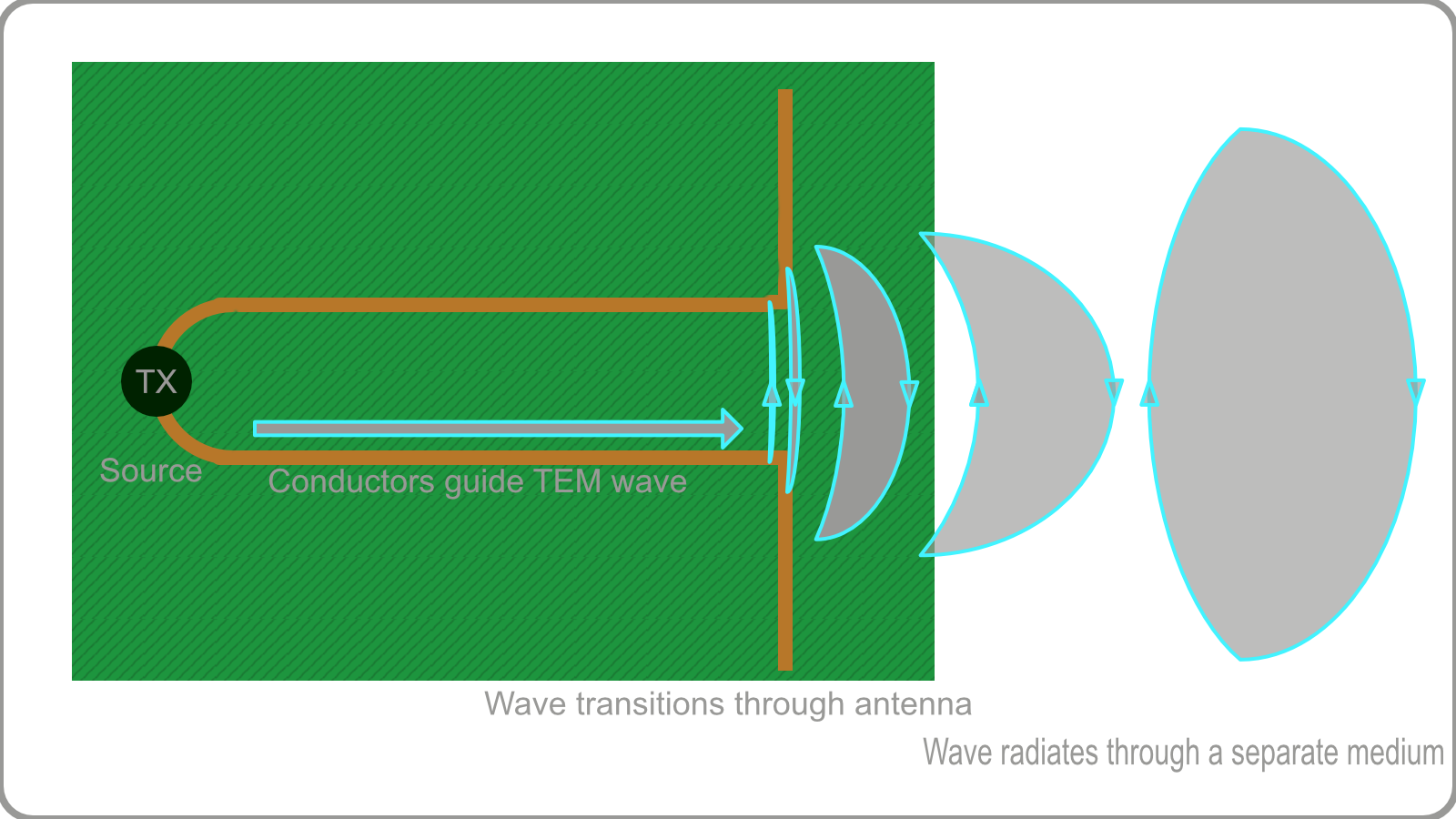
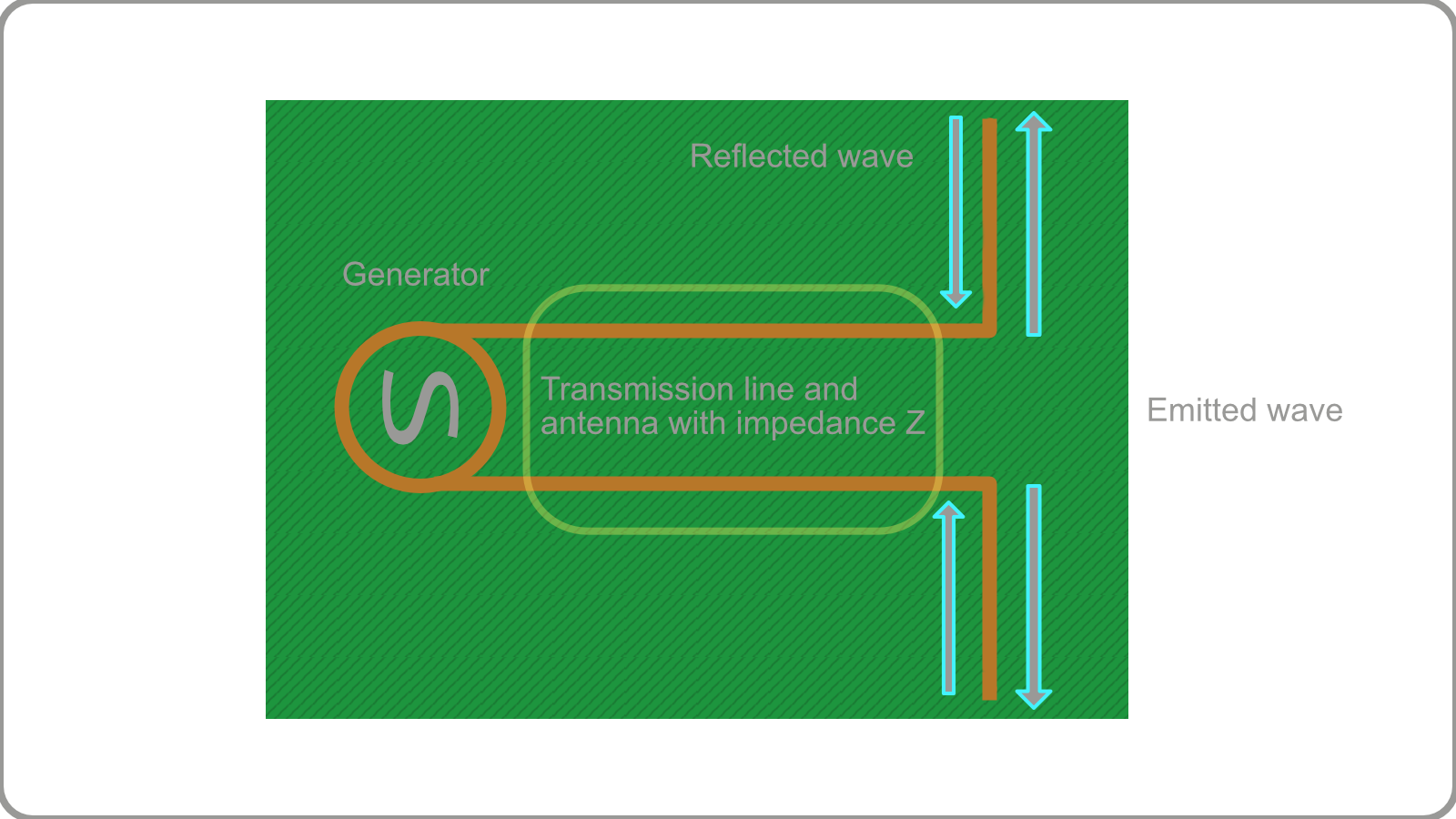
Figure 2 makes the relationship between antennas and transmission lines as members of an electric circuit appear more explicit. The key difference in our analysis is that antennas are characterized by radiation patterns. Though the patterns usually do not appear in a circuit diagrams. Already, we can tell from this figure that if we were to complete the circuit with a transmitter and a receiver, we would expect there to be some kind of power required to transport the waves.
Radiation Patterns
A Radiation Pattern (or Antenna Pattern) represents the magnitude of the electric or magnetic field as a function of angular space. As a consequence, these patterns involve the variation of power as a function of the angular quantities Θ and Φ. Figure 4 shows three diagrams of the same field pattern. Notice in (c) as Θ approaches the center, the stronger the dB pattern becomes. We can find that decibel field strength by using Equation 1:
Equation 1 $$dB = 10 log_{10}(P_{n})$$
$P_{n} = $ normalized power
$DB = $ power measured in decibels
Maxwell’s Equations in Brief
We define electromagnetic power as the product of the electric field multiplied by the magnetic field in this way:
Equation 2 $$\textbf{W}=\textbf{E} \times \textbf{H}$$
$\textbf{W}$ = instantaneous Poynting vector $[\frac{W}{m^2}]$
$\textbf{E}$ = instantaneous Electric Field Intensity $[\frac{V}{m}]$
$\textbf{H}$ = instantaneous Magnetic Field Intensity $[\frac{A}{m}]$
It’s more useful to analyze the power density crossing an enclosed space. That power density is called the Poynting vector. We then want to know the average Poynting vector as a function of time and frequency. When we take the power density multiplied per unit solid angle (a cone-like angle taken from a sphere), we obtain the radiation intensity. See Figure 3:

The radiation intensity can be represented in this way:
Equation a $$U = r^2 W_{rad}$$
$U = $ Radiation Intensity $[\frac{W}{\text{unit solid angle}}]$
$W_{rad} = $ Radiation Density $[\frac{W}{m^2}]$
The radiation intensity of an isotropic (nearly spherical) source is found to be:
Equation b $$U_0 = \frac{P_{rad}}{4\pi}$$
Antenna Directivity and Gain
There are two important figures of merit when it comes to antennas the antenna Directivity and its Gain.
Directivity
IEEE and together with the International Electrotechnical Commission (IEC) has determined that the definition of directivity should be the ratio of the radiation intensity in a given direction from the antenna to the radiation intensity averaged over all directions. The average radiation intensity is equal to the total power radiated by the antenna divided by 4π. If the direction is not specified, the direction of maximum radiation intensity is implied.[5] Equation 3 demonstrates this relationship by combining Equation a and Equation b:
Equation 3 $$D=\frac{U}{U_0} = \frac{4\pi}{P_{rad}}$$
$D = $ Directivity
$U = $ Radiation Intensity
$U_0 = $ Radiation Intensity of isotropic source
$P_{rad} = $ Total Radiated Power
The 4π value is not arbitrary. Whenever we compute the directivity we are comparing the radiation patter from the antenna being analyzed with a perfect dipole antenna. The radiation pattern that emits from a perfect dipole is called an isotropic pattern. Isotropic patterns are almost completely spherical, hence the 4π value. The Directivity of an isotropic radiation pattern is 1 (also called unity). The Directivity of any other radiation pattern is always greater than or equal to 0 and less than or equal to the Maximum Directivity. The Maximum Directivity is a type of Directivity in that it is a measure of the absolute maximum of radiation intensity (W per unit solid angle) over the radiation intensity of an isotropic source.
For a given antenna, the directivity of the radiation emitted by that antenna described in Equation 3 can be approximated by the Maximum Directivity as shown by Equation 4 and where Figure 4 is the geometric description of the radiation pattern. [2].
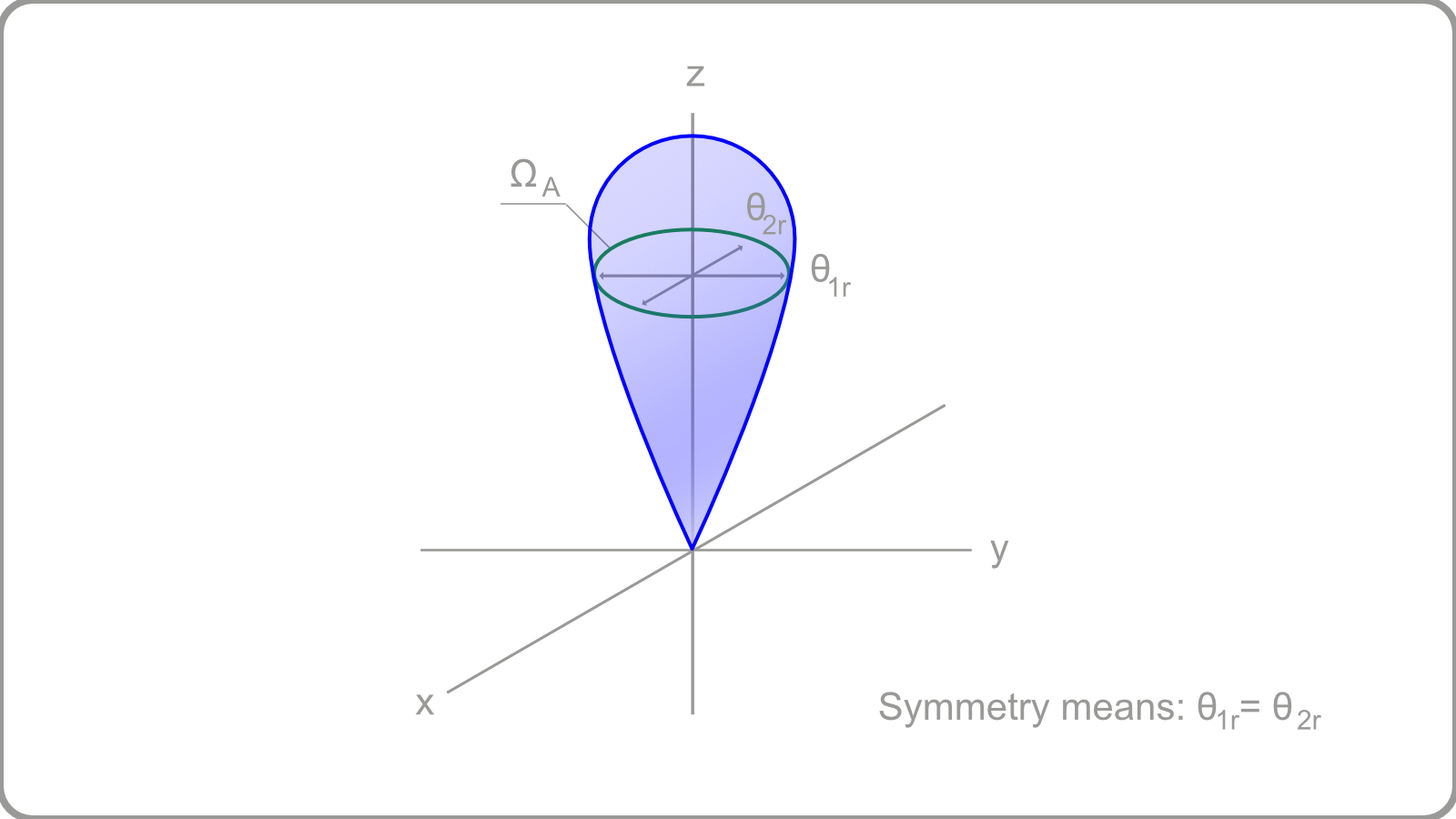
Equation 4 $$D_0 = \frac{4\pi}{\Omega_{A}} \approx \frac{4\pi}{\theta_{1r} \theta_{2r}} = \frac{4\pi}{\Omega_{A}} \sim \frac{41,253}{\theta_{1d} \theta_{2d}}$$
$D = $ Maximum Directivity
$\Omega_A = $ Solid Angle
$\theta_{1d} = $ half-power beamwidth in one plane measured in degrees ($\theta_{1r}$ is the half-power beamwidth measured in radians)
$\theta_{2d} = $ half-power beamwidth in a perpedicular plane to $\theta_{1d}$
Gain
Directivity describes the directional properties of the antenna and is directly correlated with the radiation pattern. The Gain of an antenna is a description of its performance. An antenna’s Gain is defined as the ratio of the intensity, in a given direction, to the radiation intensity that would be obtained if the power accepted by the antenna were radiated isotropically. The radiation intensity corresponding to the isotropically radiated power is equal to the power accepted (input) by the antenna divided by 4pi. (See second paragraph of section 2.9 page 61 of [2]) However, we usually deal with the Maximized Realized Gain. (Most people mean Maximized Realized Gain when they write or talk about an antenna’s gain but they generally say, “Gain”). The Relative Gain can be described by Equation 5:
Equation 5 $$G_{re0} = e_0 D_0$$
$G_{re0} = $ Maximum Realized Gain
$e_0 = $ Antenna Radiation Efficiency
$D_0 = $ Maximum Directivity
Gain is usually given in dB:
$G_{re0}=10\log_{10}{e_{0}D_0}$
The efficiency $e_0$ refers to the conduction of the antenna and the ability for the dielectric material to transport the wave as well as the reflection coefficient of the transmission line with the line elements. Equation 6 shows how all these efficiencies are related:
Equation 6 $$e_0 = e_r e_c e_d$$
$e_0 = $ Total Efficiency
$e_r = $ Mismatched Reflection Efficiency ($1-|\Gamma|^2$)
$e_c = $ Conduction Efficiency
$e_d = $ Dielectric Efficiency
Most of the time we use Equation 7 to find an approximate value of the Gain of an antenna:
Equation 7: Common Approximation of Gain $$G_0 = \frac{30,000}{\theta_{1d} \theta_{2d}} = \frac{30,000}{ \text{Beamwidth measured in degrees}^2 }$$ Equation 7: Common Approximation of Gain in dB $$G_0 = 10 \log_{10} \left( \frac{30,000}{\theta_{1d} \theta_{2d}} \right) = 10 \log_{10} \left( \frac{30,000}{\text{Beamwidth}^2} \right)$$
Where the values the combination of $\theta_{1d}$ and $\theta_{2d}$ make up the square of the Beamwidth.
Finally, there is one more approximation we can make that can get the Beamwidth which is common to obtain in
Equation 8: Common Approximation of Beamwidth measured in degrees $$Beamwidth = \frac{75 \lambda}{D}$$
$\lambda = $ Wavelength of emitted wave
$D = $ Size of the antenna
Signal to Noise Ratio
The Signal to Noise Ratio (SNR) was discovered simultaneously by many people and has many different interpretations. Personally, I regard the SNR as one of the most important analytical topics in a communication system. The reason is simple, the SNR is generally the first step to solve the problem of whether a message will be successfully received by the receiver. A rule of thumb is that an SNR of 10[dB] is a minimum requirement of what’s needed to successfully receive messages.
What we intend to transmit through an antenna is not the only radiation that is emitted, there is also unintentional radiation we call noise. Additionally, the transmitted waves are not the only waves that are received by the receiving antenna. In fact, an antenna will conduct any electromagnetic wave whose wavelength fits its profile. The signal to noise ratio is a unitless number which compares the unwanted waves (the noise) with the intended waves (the signal).
The SNR is highly influenced by the position of the receiver relative to the transmitter and its radiation pattern. For example, a receiver which sits at the null of the radiation pattern will have a signal value of zero and so the SNR will also be zero. If we position the receiver within the main lobe of the transmitter, the SNR will increase assuming the noise value remains constant.
Noise is a very in-depth topic which would be too long to discuss in this page. A good starting place though, is assuming that the only noise is thermal. That noise is represented by Equation 9 (see [6]):
Equation 9 $$P_{N} = k T B$$
$P_N = $ Thermal Noise Power
$k = 1.38 \times 10^{-23} \left[ \frac{J}{k} \right] $ Bolzmann's Constant
$T = $ Noise Temperature (in kelvins)
$B = $ Bandwidth
In a later page I will combine all these terms in a concept called the Link Budget in more detail. In this page I will mention design concerns here briefly.
- Baseband SNR or BER should be specified first
- SNR and Bit Error Rate (BER) are measured at the output of demodulator.
- The carrier power (received power at the receiver) to noise ratio (CNR) at the receiver input will determine output of SNR or BER at the transmitter. NOTE: in FM and PSK, radio frequency power is independent of modulation
- We design for required CNR in the IF section of the receiver
Working Example
A simplified (and yet, highly realistic) example should demonstrate all the Figure-of-Merit working together to analyze an antenna system.
Suppose we need analyze an antenna system where the transmitter subtends a receiver in a $17 \degree$ area. The communication uses a 4[GHz] antenna. What is the antenna's minimum Size, Directivity and Gain? (See Figure 5 )
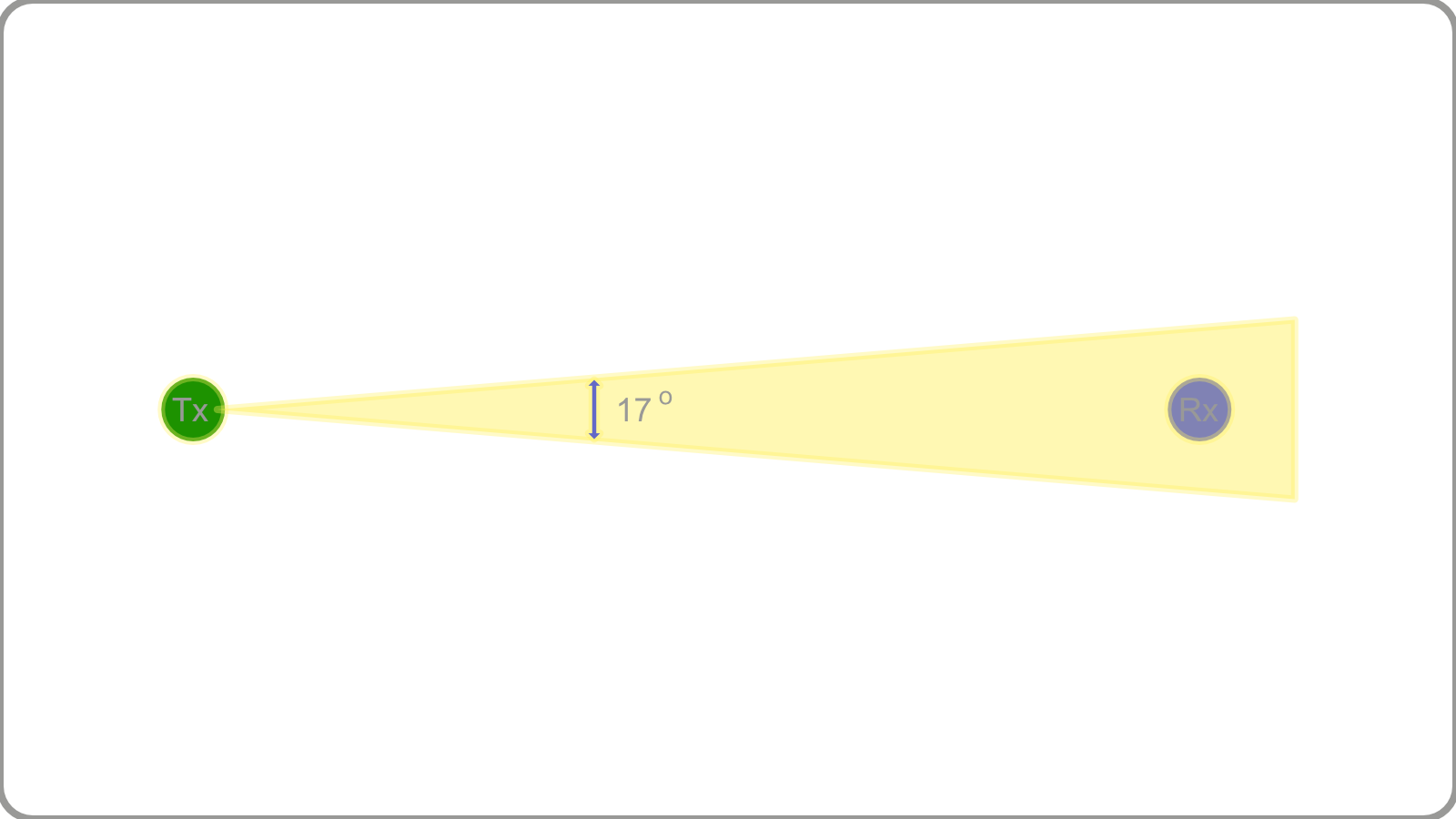
We need to first find the wavelength. As we know wavelngth is related to frequency as a fraction of the speed of light: $$\lambda = \frac{c}{f}$$
$c = 3 \times 10^8 \left[ \frac{m}{s} \right]$ Speed of light
$f = $ frequency
So now we have, $\frac{3 \times 10^8}{4 \times 10^9} = 0.075[m]$ Thus, the antenna must have an aperture of at least $D = \frac{75 \times 0.075}{17} = 33[cm]$.
To find the Gain of the antenna, we can simply use Equation 5. $Beamwidth = 17 \times 17 = 289$ and thus, $G = 10\log_{10}(\frac{30,000}{289}) = 20dB$
A Quick Claculator for Figures-of-Merit
Below is an interactive calculator that solves for antenna figures-of-merit for a two antenna system. (A single transmitter and a single receiver.) I have greatly simplified noise to a fairly good estimation, but I do not allow the user to change temperature. It should still serve as a good estimator. (See slide 4.46 of [6] also noise information by Polar in chapter 3 and 4 of [4])
Carrier Power (C) =
CNR =
Total Loss =
Noise =
Path Loss =
References
[1] J.D. Kraus, Antennas 2nd ed., McGraw-Hill inc 1988
[2] C.A. Balanis, Antenna Theory Analysis and Design 4th ed., Wiley, 2016
[3] W.H. Hayt and J.A. Buck, Engineering Electromagnetics 8th ed., McGraw-Hill 2016
[4] D.M. Pozar, Microwave and RF Wireless Systems, John Wiley & Sons, 2001
[5] "IEEE Standard for Definitions of Terms for Antennas," in IEEE Std 145-2013 (Revision of IEEE Std 145-1993) , vol., no., pp.1-50, 6 March 2014, doi: 10.1109/IEEESTD.2014.6758443. Click here for the page
[6] T. Pratt, Lecture Notes for Elec. Engr. 5656, University Printing Services Virginia Polytechnic Institute and State University, 1998
Description
This program discusses the relationship between power, gain, and signal to noise ratio when discussing wireless communication systems.